I have managed to play what I believe to be the longest possible non-trivial game of Absurdle.

What is Absurdle (and what is Wordle)?

Wordle is a game by Josh Wardle, in which you try to guess the secret five-letter word of the day. You have 6 guesses, and each time you make a guess, the game colors each of your letters either black ⬛️, yellow 🟨, or green 🟩. A green letter means that you got that letter in the right position - i.e. a green a in the third position means the secret word must have a as its third letter. A yellow letter means that letter exists in the word, but not in that position - i.e. a yellow b in the first position means the secret has a b in it somewhere, just not in the first position.

Absurdle has nearly identical mechanics, except that the game will retroactively change the secret (or, actually, list of secrets) on each turn to make it as hard as possible for you:

Wordle picks a single secret word at the beginning of the game, and then you have to guess it. Absurdle gives the impression of picking a single secret word, but instead what it actually does is consider the entire list of all possible secret words which conform to your guesses so far. Each time you guess, Absurdle prunes its internal list as little as possible, attempting to intentionally prolong the game as much as possible.

(from qntm’s description of Absurdle.)

Both Wordle and Absurdle use the same dictionaries: the secrets come from a list of 2315 common five-letter words (people would be mad if the secret word were alaap), but the player is allowed to guess words contained within a larger, 12972-word list.

Why search for the longest game?

Isn’t the point of Absurdle to get the shortest possible game? I guess that’s sort of implied, but nowhere in the rules does it explicitly say that lower is better. Someone already has a rough proof that 4 turns is the shortest possible Absurdle game, and 4-turn games have already been found. Why not go the other direction?

Defining trivial

I said that I’ve found the longest possible non-trivial game of Absurdle. By “non-trivial”, I mean:

1. each word played is unique
2. each guess would be a valid guess under Wordle’s hard mode.

Without the first rule, it’s easy to see that you could make an arbitrarily long Absurdle play: Absurdle doesn’t prevent you from guessing the same word twice, so you can just repeat some guess as many times as you like.

The second rule may be a little less obvious, but is still important to make this challenge interesting. Without the second rule, you could play an Absurdle game of length 12972 (the length of the dictionary) by following these steps:

1. Play Absurdle like normal, until you have narrowed down the set of possible secrets to a single word.
2. Guess every word in the dictionary that isn’t that single word, and that you haven’t guessed so far.
3. Finally, guess the correct word.

Hard mode rules

Absurdle doesn’t actually have a hard mode, but since it’s otherwise consistent with Wordle, I’m assuming that if it did have a hard mode, it would work the same as Wordle.

Under Wordle’s hard mode, your guesses must:

• include each of the green letters you have discovered, in the position where you found them.
• include each of the yellow letters you have discovered somewhere in the word.

If the secret contains multiple copies of a letter, it’s possible to get multiple yellows or a green + yellow for the same letter. If your guess contains more copies of a letter than the secret has, the excess copies will be black (or white, if you use light mode.) For example, if the secret is abbey and you guess babka, your clue would be 🟨🟨🟩⬛️⬛️. This indicates that there are two bs, one in the third position, and the other one in the 2nd, 4th, or 5th position; it also indicates that there is only one a.

If you were playing the example above in hard mode, any future guesses must include a b at the third position, an additional b somewhere else, and an a somewhere else.

Hard mode does not enforce the following rules that you might expect:

• that you play yellow clues somewhere other than where you found them. e.g. in the abbey/babka example, we know that the secret does not start with ba, but Wordle will still let us guess babes.
• that your guesses do not contain the letters that you have eliminated with ⬛️. e.g. in the abbey/babka example, we could still guess kebab even though we know that the secret has no k.

Finding the best secret

With the insight that a long game is always going to start with a long string of ⬛️⬛️⬛️⬛️⬛️ clues, I initially planned to split my search in to two phases:

1. Find sequences of guesses that narrow Absurdle’s internal secret list to a single word with only ⬛️⬛️⬛️⬛️⬛️ clues.
2. Once you have a secret, find the maximum length of play you can make for that secret.

My code for finding sequences of ⬛️⬛️⬛️⬛️⬛️ that end up at each of the 2315 possible secrets was taking a long time, so I decided to start the other way around: Assuming that I can find an all-black path to each secret, calculate the maximum length of game for that secret.

First-order heuristic: number of guesses with no letters in common with each secret

Since the first phase of the long play is going to be a bunch of ⬛️⬛️⬛️⬛️⬛️, I calculated how long this phase could be for each secret:

577 arose
626 arise
626 raise
697 aisle
749 yeast
759 aside
762 sepia
789 saute
823 saner
823 snare
...
6899 fizzy
6923 puffy
6928 jiffy
6975 chuck
7344 vivid
7409 fluff
7571 mummy
7571 puppy
7598 civic
7875 fuzzy

This means if we force Absurdle to narrow down the list of secrets to arose, there are 577 words we can play that don’t contain a, r, o, s, or e. If the secret is fuzzy, there are 7875 words that don’t contain f, u, z, or y.

Second-order: one letter in common

Once we’ve played all our ⬛️⬛️⬛️⬛️⬛️, we aren’t done. What if we chose a letter, and played all the words that have that letter in common with the secret? We could play all the words that would keep that letter yellow, then give up and turn that letter green.

If our secret is fuzzy, maybe we choose u to turn yellow. We could then play all the words that have a u in the first, third, fourth, or fifth positions, but no other letters in common with fuzzy. Furthermore, once we’ve done that, we could turn the u green, and play all the words that have u in the second position.

Our second-order heuristic is then:

1. count the number of ⬛️⬛️⬛️⬛️⬛️ words for each secret
2. For each of the single letters (ignore any letters that are doubled for now, since that seems complicated to deal with), count the number of additional words that unlocks.
3. Choose the best single letter from step 2, and add that count to the count from step 1.

Here are the scores under the second-order heuristic:

1514 rose arose
1586 aris arise
1586 rais raise
1857 aisl aisle
1950 side aside
1968 tare stare
1995 aner saner
1995 nare snare
2099 spia sepia
2132 last least
...
9333 mmmy mummy
9389 pppy poppy
9389 pppy puppy
9518 whff whiff
9649 bbby bobby
9751 fuff fluff
9785 fzzy fizzy
9785 fzzy fuzzy
9861 jffy jiffy
10355 jzzy jazzy

(The second column is the secret with the chosen letter dropped; my implementation effectively checks all the possible guesses against this shorter “secret”.)

This changes the order of the secrets dramatically, bringing jazzy from 45th place with 5968 ⬛️⬛️⬛️⬛️⬛️s all the way to first place with 10355 words with ⬛️⬛️⬛️⬛️⬛️ or a yellow or green a.

It also makes fizzy and fuzzy equivalent - fizzy has 6899 ⬛️⬛️⬛️⬛️⬛️ words, but then you can play 2886 words containing i. fuzzy has 7875 ⬛️⬛️⬛️⬛️⬛️ words, but then you can play 1910 words that contain a u.

Nth-order: recursively searching for the best play per secret

How many words can we play if we recursively apply the strategy above? Once we’ve picked a letter to turn yellow and then green, what’s the best next letter?

Furthermore, what if it’s actually better to e.g. leave that letter yellow, turn another letter yellow, and get all the words that contain that pair of letters? This would be better if there are more words that contain that pair of letters (in places different than in the secret) than words that have the first letter in exactly the same spot. (This turns out to be true for affix: it’s better to have yellow a and yellow i than a green a.)

I wrote some code that recursively:

• groups all remaining guesses (guesses that haven’t been ruled out by hard mode rules) by the hint they would give you.
• For each of those hints:
  • count the number of guesses that give you the same hint
  • Recurse, and add the returned score to the count from the previous step
• return the best score we saw among all the hints.

With some additional bookkeeping, we can make this give us the best score as well as the path (sequence of hints) to reach that path.

Under this metric, here are the worst and best secrets:

saner 2598 <.....,> <.....,s> <.....,es> <...e.,s> <...e.,sa> <.a.e.,s> <.a.e.,rs> <.a.er,s> <sa.er,> <saner,>
stare 2615 <.....,> <.....,s> <.....,es> <.....,ers> <s....,er> <s..r.,e> <s..re,> <s..re,a> <s.are,> <stare,>
arose 2669 <.....,> <.....,a> <.....,sa> <.....,esa> <.....,ersa> <....e,rsa> <...se,ra> <.r.se,a> <ar.se,> <arose,>
snare 2669 <.....,> <.....,s> <.....,es> <.....,ers> <s....,er> <s..r.,e> <s..re,> <s..re,a> <s.are,> <snare,>
slate 2696 <.....,> <.....,e> <.....,es> <s....,e> <s...e,> <s...e,a> <s.a.e,> <s.a.e,t> <s.ate,> <slate,>
stale 2696 <.....,> <.....,e> <.....,es> <s....,e> <s...e,> <s...e,a> <s.a.e,> <s.a.e,t> <sta.e,> <stale,>
raise 2703 <.....,> <.....,s> <.....,es> <.....,esa> <.a...,es> <.a...,ers> <ra...,es> <ra.se,> <raise,>
arise 2741 <.....,> <.....,s> <.....,sa> <.....,esa> <.....,ersa> <....e,rsa> <...se,ra> <.r.se,a> <ar.se,> <arise,>
aisle 2862 <.....,> <.....,s> <.....,sa> <.....,esa> <....e,sa> <....e,lsa> <...le,sa> <..sle,a> <aisle,>
sepia 2897 <.....,> <.....,a> <.....,sa> <.....,esa> <s....,ea> <se...,a> <se..a,> <se..a,i> <sepia,>
...
whiff 9680 <.....,> <.....,i> <..i..,> <..i..,h> <.hi..,> <whi..,> <whif.,> <whiff,>
poppy 9730 <.....,> <.....,o> <.o...,> <.o...,y> <.o..y,> <po..y,> <po.py,> <poppy,>
civic 9853 <.....,> <.....,i> <.i...,> <.i...,c> <ci...,> <civ..,> <civi.,> <civic,>
fluff 9872 <.....,> <.....,l> <.l...,> <.l...,u> <.lu..,> <flu..,> <fluff,>
fizzy 9966 <.....,> <.....,i> <.i...,> <.i...,y> <.i..y,> <.i..y,f> <fi..y,> <fizzy,>
bobby 9995 <.....,> <.....,o> <.o...,> <.o...,y> <.o..y,> <bo..y,> <bo.by,> <bobby,>
fuzzy 10014 <.....,> <.....,u> <.u...,> <.u...,y> <.u..y,> <.u..y,f> <fu..y,> <fu.zy,> <fuzzy,>
jiffy 10048 <.....,> <.....,i> <.i...,> <.i...,y> <.i..y,> <.i..y,f> <.if.y,> <.if.y,f> <.iffy,> <jiffy,>
mamma 10554 <.....,> <.....,a> <.a...,> <.a...,a> <.a..a,> <ma..a,> <mam.a,> <mamma,>
jazzy 10692 <.....,> <.....,a> <.a...,> <.a...,y> <.a..y,> <ja..y,> <jazzy,>

(The notation here is: green letters before the comma, yellow letters after. e.g. <s...e,a> is a green s in position 1, green e in position 5, and a yellow a somewhere else.)

This doesn’t change the numbers too dramatically compared to the 2nd-order heuristic, though it does bring mamma up to 2nd place. My 2nd-order heuristic ignored mamma because it didn’t handle double letters. It also makes fizzy and fuzzy no longer equivalent: once you’ve played the i or u, the set of allowed guesses are different.

Going back to our overall strategy, this should mean that if we can find a sequence of guesses that give us ⬛️⬛️⬛️⬛️⬛️ and narrow down the set of words to just jazzy, we can construct our maximally-long play.

Finding a path to jazzy

To find our path to jazzy, we’ll use recursion again.

• for all possible guesses:
  • if Absurdle would give us ⬛️⬛️⬛️⬛️⬛️ for that guess, and the guess contains at least one letter we haven’t guessed so far:
    • figure out the set of secrets remaining once we play that guess
    • if that set of secrets still contains jazzy:
      • recurse

I ran this for a few minutes, and it found oiler, munts, coked, beech.

We can double-check that this sequence of guesses does force Absurdle to having jazzy as its only secret, with no green or yellow clues (except for jazzy).

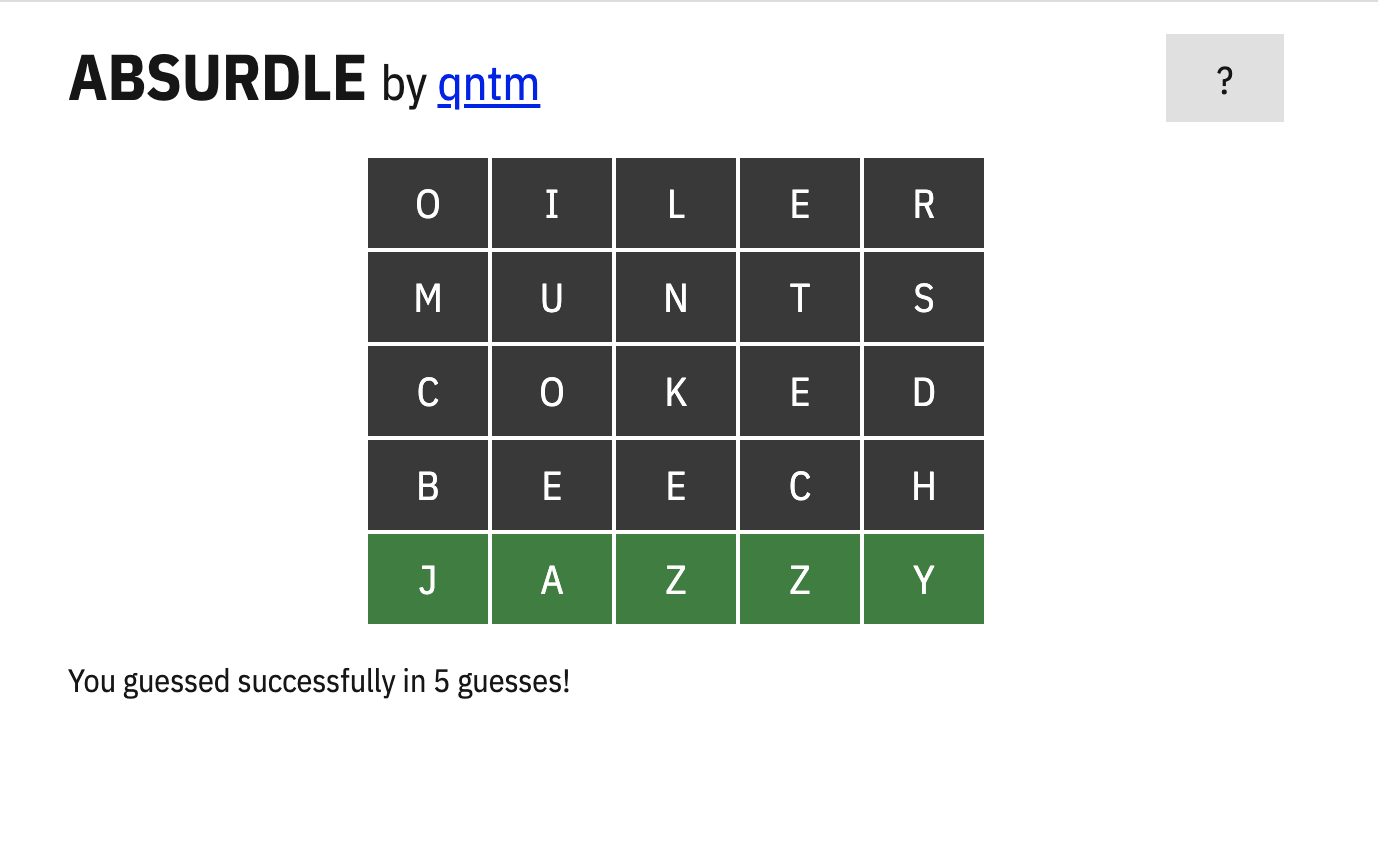
Constructing our longest play

Now, to construct our play, we need to start with oiler, munts, coked, beech

Then, for the optimal sequence of hints we found: <.....,> <.....,a> <.a...,> <.a...,y> <.a..y,> <ja..y,> <jazzy,>

we need to loop over these hints, and find all the guesses (that we haven’t already guessed) that would give the same hint. This gives us a list of 10692 words, starting with oiler and ending with jazzy.

Actually playing this list

I constructed some javascript that can be pasted into the developer tools console on the Absurdle page. (Please don’t judge my JS skills too harshly, it’s been a long time since I wrote Javascript professionally.) This took several hours to run (I suspect Absurdle isn’t optimized for long games like this) but ultimately succeeded: